The Case for Enlarging the House of Representatives

1. Wyoming Rule: Add 139 Seats

The Wyoming Rule calls for increasing the size of the House to bring the average representative-to-constituent ratio as close as possible to that of the least populous state, which is currently Wyoming. Every ten years, the formula would be adjusted based on the population of the least populous state, and the size of the House would be adjusted accordingly. Based on the 2020 census, implementation of the Wyoming Rule would increase the House to 574 seats, leaving every state other than Wyoming, Alaska, North Dakota, and Vermont with at least two representatives. Nationwide, each representative would have an average of 572,000 constituents, helping end representation disparities and bringing Congress closer to the ideal of “one person, one vote.”

A potential problem with the Wyoming Rule is that if the population of the smallest states increased, constituent-to-representative ratios would increase nationwide. Conversely, if the population of the smallest state decreased, the size of the House might increase dramatically. In short, pegging the ratio to a varying denominator would generate instability in House and district size. Under some apportionment years (most recently 1990), enactment of the Wyoming Rule could have resulted in wider disparities between states. Implementation of this proposal would need to be combined with other proposals to ensure it fulfills its mission of reducing state representation disparities.

2. Cube Root Law: Add 258 Seats

In many nations, the number of seats in the lower legislative chamber adheres roughly to the cube root of the population. The cube root of a number is a smaller number that, multiplied by itself three times, produces the number. For example, the cube root of 8 is 2, because 2 x 2 x 2 = 8. The cube root of 331,449,281 (the U.S. population according to the 2020 census) is 692.05. Under the Cube Root Law, the U.S. House would have 692 seats.

As explained in greater detail in Part VI, the cube root is a fairly strong indicator of the size of lower legislative chambers across global democracies. In fact, the United States has one of the largest gaps between chamber size and the cube root of its population. Implementation of the Cube Root Law would result in an adjustment of the size of the House every ten years based on population.

Detractors point to a few issues with the Cube Root Law, particularly the fact that its initial implementation would add too many seats to the House at once (a critique that would also apply to all of the other proposals outlined below). This could be mitigated by adopting a formula of expansion that would bring the House in line with the cube root of the population gradually. Another concern is district size. Following the one-time addition of seats to bring the House in line with the cube root, future expansions would still result in an increase in average district size over time.45 A final concern is one of messaging: because it uses a formula based on mathematical calculation, the Cube Root Law is simply not as easy to market to lawmakers or the American public as some of the other proposals for House expansion.

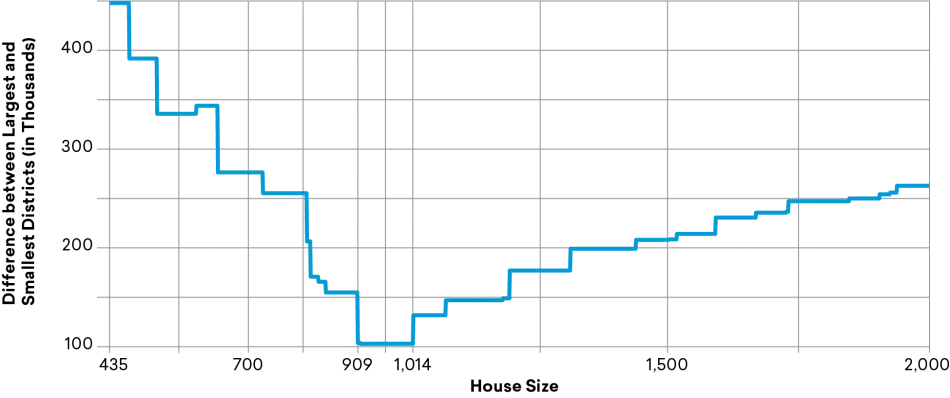
3. Least Variation: Add between 474 and 579 Seats

The current apportionment method results in disparities between state representative ratios. Rhode Island’s population is only slightly larger than Montana’s but, under the 2010 apportionment, Rhode Island had two seats while Montana had one, meaning Rhode Island representatives had almost half the number of constituents as Montana’s lone congressperson. In Wesberry v. Sanders (1963), the Supreme Court ruled that, within states, districts must be roughly equal in population. Could the same standard be applied across states? Based on the 2020 census, the ideal size for least variation would be a House between 909 and 1,014 seats, which would mean each representative averaged between 364,000 and 326,000 constituents.

Such an expansion, though, would be too large to sell politically. The appeal of this proposal is to reduce variation as much as possible but, in most circumstances, the Wyoming Rule represents a more feasible solution to expand the House while ensuring relatively even district size.

4. Restore Historical Ratios: Add 1,165/6,065/8,965 Seats

In the 1st Congress, each representative had about 35,000 constituents. Under James Madison’s first proposed amendment to the Constitution, once the House reached 200 members, it would retain a ratio of 50,000 people per representative. In 1913, when the House was expanded to 435, each representative had 211,000 constituents. Restoring any of these formulas would entail a dramatic expansion that would bring the House closer in line with the vision of the nation’s founders. A return to the 1790 ratio would yield a House of roughly 9,400 seats; Madison’s first amendment would yield roughly 6,500 seats; while the 1913 ratio would yield roughly 1,600 seats.

Arguments against these proposals are fairly simple: each would be too dramatic of an expansion to be feasible. While they would restore one founder’s vision of the chamber, an expansion to a House of more than 1,000 seats would need to be undertaken extremely gradually and with a dramatic rethinking of how the chamber functions.

Figure 2

Gap between Largest and Smallest Districts by Potential House Size

Source: Author calculations of projected district allocation and size based on 2020 census data using the Huntington-Hill method.

Endnotes

45Caroline Kane, Gianni Mascioli, Michael McGarry, and Meira Nagel, Why the House of Representatives Must Be Expanded and How Today’s Congress Can Make It Happen (New York: Democracy and the Constitution Clinic, Fordham University School of Law, 2020), 13.