Redistricting and Representation

I want to welcome you all to this fascinating symposium hosted by the American Academy of Arts and Sciences on the topic of Redistricting and Representation. Let me begin by thanking the Academy for sponsoring so many different programs ranging from philosophy to science to law to nuclear war to education. Name a cutting-edge topic and the Academy is addressing it.

Today’s topic on partisan gerrymandering spans issues of law, mathematics, and policy. The term “gerrymander” was coined after our own Elbridge Gerry, Governor of Massachusetts, who signed an 1812 law that included a voting district shaped like a salamander to help his party. Tonight’s program is not about an esoteric topic, but one that is on the front burner of the Supreme Court in the landmark case of Gill v. Whitford, which was just argued before the Court on October 3, 2017. A split three-judge federal court in Wisconsin had invalidated a redistricting act passed by the Wisconsin legislature on the grounds that partisan gerrymandering violated the Equal Protection Clause. The Court found that the act was intended to burden the representative rights of Democrats by impeding their ability to translate their votes into seats, that it had its intended effect, and that the plan was not explained by the political geography of Wisconsin and was not justified by a legitimate state interest. There was a four-day trial with eight witnesses. This was the first decision in decades to reject a voting map as an unconstitutional partisan gerrymander.

As background, the Constitution requires that states must make a good faith effort to achieve precise mathematical population equality in Congressional districting, and the Equal Protection Clause of the Fourteenth Amendment requires the same in drawing lines for seats in the state legislature. Most of you know that legal principle as one person, one vote. In addition, both the Constitution and the Voting Rights Act prohibit racial gerrymandering. What makes the Gill v. Whitford case so unusual is that it involves partisan gerrymandering, which means–loosely speaking–the common practice of the party in power to choose the redistricting plan that gives it an advantage in the polls.1 The Supreme Court has tackled this issue before in fractured decisions and rejected the challenges, but some justices left open the possibility that such challenges were justiciable and manageable.

The debate before the Supreme Court was robust. Was this an equal protection problem? Was it a First Amendment question involving freedom of speech and association? Are there metrics like the so-called efficiency gap that make it feasible for federal courts to decide? At the oral argument, Chief Justice Roberts worried that the Supreme Court would have to decide in every case whether the Democrats or the Republicans would win, and “that is going to cause very serious harm to the status and integrity of the decisions of this Court in the eyes of the country.”

I do not have answers to these three questions but hopefully our wonderful panelists will address the issues.

Endnotes

• 1Davis v. Bandemer, 478 U.S. 109, 164 (1986).

In 1986, the U.S. Supreme Court declared political gerrymandering justiciable, which means that a plaintiff can ask the courts to throw out a legislative redistricting plan if the plan treats one of the parties unfairly. Since then, however, political gerrymandering has never been justished (OK, that’s my word!), meaning that no plan has ever in fact been thrown out, nor has the Court established the standard that redistricting plans must meet.

So that was 1986. What was happening in 1987? Well, the most important thing going on then, from my point of view, was that I really wanted a job. The university down the road gave me an interview and the chance to give a job talk.1 I discussed an article that was to be published that year in the American Political Science Review with my graduate school buddy Robert Browning.2 In that article, we proposed a mathematical standard for partisan fairness and a statistical method to determine whether a redistricting plan meets that standard. We called the standard partisan symmetry.

As it has turned out, I am proud to say that since our article and my job talk, virtually all academics writing about the subject have adopted partisan symmetry as the right standard for partisan fairness in legislative redistricting.

Then, a little more than a decade ago, the Supreme Court actually said in an opinion (roughly!), hey you academics out there, if there were some standard that you all agreed on, we would love to hear about it. This led me to think, job talk time again!

So in the next redistricting case that reached the Court, my friend Bernie Grofman and I, along with a few others, filed an amicus brief telling the Court all about partisan symmetry.3 By that time, partisan symmetry was not merely the near universally agreed upon standard among academics; it had also become the standard used by most expert witnesses in litigation about partisan gerrymandering. In fact, in many cases, including the one for which we filed the brief with the Supreme Court, experts on both sides of the same cases appealed to partisan symmetry.

The Supreme Court explicitly discussed our brief in three of its opinions, including the plurality opinion. All of the justices’ discussions in their opinions of our brief, and the partisan symmetry standard, were positive. It appeared that, if a redistricting plan were ever overturned, the standard adopted by the Court would have to involve partisan symmetry. But the justices in that case did not go so far as to overturn the redistricting plan before it, or to explicitly adopt a standard for future cases.4

Since 1987, data on voters have gotten better. The science has advanced. Statistical methods used to determine whether a plan meets the standard have improved. With high accuracy, we can now determine whether an electoral system meets the partisan symmetry standard after a set of elections, after just one election, or, without much loss of accuracy, before any elections have been held at all. These methods have been rigorously tested in thousands of elections all over the world. The standards are clear and the empirical methods are ready.5

Now along comes a new Supreme Court case, Gill v. Whitford. With a few colleagues, I filed a new brief in that case, reminding the justices about partisan symmetry and clarifying some other issues.6 The case has not yet been decided, but judging from the oral arguments last month, partisan symmetry is again a central focus. By the way, I highly recommend listening to the oral arguments; they were remarkably sophisticated and intense, quite like a high-level seminar at a leading university. (Although beware, and much to my chagrin, all references to “Professor King’s brief” in the oral arguments were to the brief I filed a decade ago, with no mention of the one I filed in this case!)

But let me say something about partisan symmetry: how it is really simple, and why you should support it too. A good example comes from the case presently before the Court. At issue is a redistricting plan passed by the state of Wisconsin in 2011.

In the 2012 election, Republicans received 48 percent of the votes statewide and, because of the way in which the districts were drawn, more than 60 percent of the seats in the state assembly. It may seem strange that the Republicans received a minority of the votes and a majority of the seats, but strange does not make it unfair. What makes it vividly unfair is the next election in Wisconsin: In 2014, the Democrats happened to have a turn at receiving about 48 percent of the votes. Yet, in that perfectly symmetric voting situation, the Democrats only received 36 percent of the seats. Moreover, we know from considerable scholarship in political science that this is not going to change. In all likelihood, no matter how many elections are held in which the Democrats happen to receive about 48 percent of the votes, they are not going to come close to having 60 percent of the seats – for as long as the districts remain the same. That’s unfair. And the reason it is unfair is because it is asymmetric.

This is a dramatic Republican gerrymander. But remember we have analyzed thousands of elections and know that the Democrats have done just as much damage when they are able to control the redistricting process.

To be clear, any translation of votes to seats is fair – as long as it is symmetric. For example, some states require redistricters to draw plans that make competitive elections likely – so 52 percent of the votes might produce 75 percent of the seats rather than say 55 percent, which is fair so long as the other party would also get 75 percent of the seats if they also got 52 percent of the votes.

Other states require redistricters to draw plans that favor incumbents, perhaps so that members of Congress from their state will have more seniority and thus influence, which will yield a result closer to proportional representation, with seat proportions closer to vote proportions.

In fact, I think I can convince you that you have already invented a symmetric electoral system when you go out to dinner with a group and need to choose a restaurant. The decision rule most people choose is called the Unit Veto system whereby any one person can veto the outcome. This decision rule is fair because it is symmetric – it is not only Bob or Sally who can veto the choice; any member of the group can. This is an extreme system, one we probably would not choose for electing members of a legislature, but it is one of the numerous possible symmetric and thus fair electoral systems.

The point is not only that partisan symmetry is the obvious standard for a fair electoral system. It is also that, if the Court adopts partisan symmetry, it will still be leaving considerable discretion to the political branches in each state, something that the Court sees as essential.

Partisan symmetry leaves redistricters lots of other types of discretion in drawing districts as well. One is compactness, which many states and federal law require. The paper I wrote with my graduate students Aaron Kaufman and Mayya Komisarchik, and distributed at this event, provides a single measure of compactness that predicts with high accuracy the level of compactness any judge, justice, or legislator sees in any district.7 There are also criteria based on maintaining local communities of interest, not splitting local political subdivisions, having equal population, not racially gerrymandering, and many others. Partisan symmetry may be related to some of these in some states but the standard does not absolutely constrain any one of these criteria.

In fact, a huge number of other factors are also chosen by redistricters, most of which no court, constitution, or legislature has ever tried to regulate, and few of which have even been written about. Moreover, these other factors could not be more important to those responsible for redistricting. None are constrained by partisan symmetry.

Here is an example. To learn about redistricting and to obtain access to data, I occasionally sign on as a statistical consultant. I estimate the deviation from partisan symmetry for every proposed redistricting plan, determine the degree of racial bias, and compute compactness, among other things.

During this process, one of the legislators was raging mad about the proposed plan, just fuming. Well, one of the things I do whenever I am near partisans and have access to data is to compute the probability that they will win the next election. It turns out these predictions are straightforward and highly accurate. Knowing these predictions helps reveal the motives, interests, and desires of most everyone. (And don’t judge: no matter how noble the goals of politicians, if they don’t first attend to their own reelection, they won’t be able to do anything else.)

So I looked up my forecasts for this apoplectic legislator and said, “what are you upset about? You are going to win this election with about 75 percent of the vote.” At that point, he was pacing and insisting, “Look at the plan, look at my district!”

So I said, “Yes, but you are going to be reelected. What do you want, 85 percent of the vote? What is the big deal?” He then explained, “Look at this line,” pointing to one of the boundaries of his district. “Do you see where it excludes this little area and then continues? That’s my kids’ school. And this? That’s where my wife works. And this? That’s my mom’s house!” He then pointed to the map on the wall of the entire state and said, “Previously I had a nice compact district where I could drive to see any constituent. Now the district is splayed halfway across the state, and it will take me all day flying to get anywhere! They are just trying to annoy me. They are trying to get me to resign!”

And they were trying to get him to resign. So we looked into it – systematically, across many elections and many redistricting plans.8 It turns out that, during redistricting, incumbents are much more likely to resign, and that causes the partisan division of seats in the legislature to be more responsive to changes in voter preferences, at least compared to no redistricting. Redistricting is a nasty process, probably the most conflictual form of regular politics this country ever sees, with a good number of fist fights, examples of hardball politics, and many really unhappy bedfellows. Imagine if some guy you don’t know in a basement playing with maps once a decade could get you fired! As a result, legislators often prefer to retire over the risk of getting drawn into a district with another incumbent, perhaps having to run against your friend, or ending a successful career being humiliated at the polls in a new district dominated by opposition party voters.

In fact, lack of redistricting does not mean no change. Voters move, die, come of age, immigrate, emigrate, and come to the polls in different numbers. Over time, without redistricting, nothing constrains the electoral system from moving far from partisan symmetry. Some states become horribly biased on their own, without moving district lines.

In contrast, if you control a state’s redistricting, you are likely to restrain yourself to some degree. Why? Well, you can gerrymander in your favor, moving your state far from symmetry, but if you go too far and wake the sleeping judicial giant, you might have the entire process taken away from you. If that happens, you lose not only the opportunity to win a few more seats for your party, but also the opportunity to have completely free reign over everything that may otherwise make your life, and that of your party members, miserable.

So redistricting increases responsiveness and reduces partisan bias relative to no redistricting at all. In that sense, aspects of messy partisan redistricting battles can be good for democracy.

But it also means that the Supreme Court can play a fundamental role and reign in much of the excesses of gerrymandering without much trouble. All they need to do is to eliminate the worst cases by adopting the partisan symmetry standard, and to outlaw the worst excesses. If the Court takes this minimal action, redistricters – jealous of their prerogatives – will stay well away from the line. Any line, even one that is not bright white, will greatly increase the fairness of American democracy. The problem here is not some foreign power meddling in our election system; the problem is on us as Americans. And the institution in American politics to fix the problem is the Supreme Court; it is the only institution capable of fixing this problem. We certainly know from two hundred years of partisan redistricting battles that no legislature will save the day.

So as I wait with the rest of the country for this Court decision, I feel a little like I am in the same position I was thirty years ago – hoping someone will like my job talk.

Endnotes

• 1Thanks to the members of the search committee: Jim Alt, Mo Fiorina, and Bob Putnam!
• 2Gary King and Robert X. Browning, “Democratic Representation and Partisan Bias in Congressional Elections,” American Political Science Review 81 (1987): 1252–1273, copy at http://j.mp/2n5Y11v.
• 3Gary King, Bernard Grofman, Andrew Gelman, and Jonathan Katz, “Brief of Amici Curiae Professors Gary King, Bernard Grofman, Andrew Gelman, and Jonathan Katz in Support of Neither Party,” U.S. Supreme Court in Jackson v. Perry, 2005, copy at http://j.mp/2gw1W1R.
• 4Bernard Grofman and Gary King, “The Future of Partisan Symmetry as a Judicial Test for Partisan Gerrymandering after LULAC v. Perry,” Election Law Journal 6 (1) (2008): 2 – 35, copy at http://j.mp/2ow4pQ8.
• 5Gary King, “Representation Through Legislative Redistricting: A Stochastic Model,” American Journal of Political Science 33 (1989): 787–824, copy at http://j.mp/2o46Gkk; Andrew Gelman and Gary King, “Estimating the Electoral Consequences of Legislative Redistricting,” Journal of the American Statistical Association 85 (1990): 274–282, copy at http://j.mp/2nRBBOO; Andrew Gelman and Gary King, “A Unified Method of Evaluating Electoral Systems and Redistricting Plans,” American Journal of Political Science 38 (1994): 514–554, copy at http://j.mp/2oT1ZqA; Stephen Ansolabehere and Gary King, “Measuring the Consequences of Delegate Selection Rules in Presidential Nominations,” Journal of Politics 52 (1990): 609–621; Gary King, “Electoral Responsiveness and Partisan Bias in Multiparty Democracies,” Legislative Studies Quarterly XV (1990): 159–181, copy at http://j.mp/2o4k5Jc; Andrew Gelman, Jonathan Katz, and Gary King, “Empirically Evaluating the Electoral College,” in Rethinking the Vote: The Politics and Prospects of American Electoral Reform, ed. Ann N. Crigler, Marion R. Just, and Edward J. McCaffery (New York: Oxford University Press, 2004), 75–88, copy at http://j.mp/2ovY86M.
• 6Heather K. Gerken, Jonathan N. Katz, Gary King, Larry J. Sabato, and Samuel S.-H. Wang, “Brief of Heather K. Gerken, Jonathan N. Katz, Gary King, Larry J. Sabato, and Samuel S.-H. Wang as Amici Curiae in Support of Appellees,” Filed with the Supreme Court of the United States in Beverly R. Gill et al. v. William Whitford et al., 2017, 16–1161, copy at http://j.mp/2iJAMZl.
• 7Aaron Kaufman, Gary King, and Mayya Komisarchik, “How to Measure Legislative District Compactness If You Only Know it When You See it,” working paper, 2017, copy at http://j.mp/2u9OWrG.
• 8Andrew Gelman and Gary King, “Enhancing Democracy Through Legislative Redistricting,” American Political Science Review 88 (1994): 541–559, copy at http://j.mp/2ow4XoP.

I want to spend my time talking about partisan gerrymandering in legal rather than social scientific terms, and why it is such a vexing issue, more vexing than it might appear on its face. I will begin by offering some remarks on the case law of the Supreme Court before discussing some of the obstacles to clear thinking in the area of partisan gerrymandering.

The Supreme Court first addressed the constitutionality of partisan gerrymandering in a 1986 case called Davis v. Bandemer. That was a case involving redistricting of the state legislature in Indiana after the 1980 census. There, Justice White said that a party could prevail on the claim by showing “intentional discrimination against an identifiable political group” and “an actual effect on that group.” Effect meant “evidence of continued frustration of the will of a majority of the voters or effective denial to a minority of voters of a fair chance to influence the political process.” This standard was borrowed essentially from racial vote dilution cases. You could show that a minority group’s right to vote was diluted if you could demonstrate intentional effort to do so and success at doing so.

In some sense, with partisan gerrymandering the intent prong is easier than with race, but the effect prong is vastly more difficult. A racial minority group is often numerically smaller than voters from one of the major political parties, and so it is easier to frustrate a racial minority group’s ability to influence the political process in a sustained way. Maybe more importantly, whether someone is a racial minority is a fixed characteristic in a way that is not true of whether someone is a Democrat or a Republican. Whether Democrats or Republicans have been denied effective participation in the political process interacts in complex ways with the substantive issues they tend to support or not support.

The Supreme Court has never held that the Davis v. Bandemer standard was satisfied. Indeed, in a 2004 case involving Pennsylvania redistricting, Vieth v. Jubelirer, four members of the Court were willing to say there is no judicially manageable standard. Justice Kennedy in that case agreed that there was no clear standard for declaring a violation in Pennsylvania, but he refused to say a standard might not develop in the future. The Wisconsin case argued last month, Gill v. Whitford, is an effort to revisit this question. The three-judge district court held that Wisconsin Republicans had created an unconstitutional partisan gerrymander, relying in part on a measure of wasted votes called the efficiency gap that I expect others to get into more deeply.

Interestingly, it appeared that every member of the Court in Vieth conceded that partisan gerrymandering was inconsistent with democracy. So if there is so much agreement as to the undemocratic nature of partisan gerrymandering, why has the Court not played a meaningful role to date?

I am going to list six obstacles and discuss each very briefly. In sum, they are: (1) constitutional design; (2) one person, one vote; (3) race; (4) what I will call the baseline problem; (5) geography; and (6) remedial concerns.

First, on constitutional design, the Constitution does not specify any particular democratic arrangement, nor does it by its terms exclude political influence over the structure of the electoral process. The manner of conducting elections for Congress, for example, is granted to state legislatures, with no explicit constitutional guidance over how to do that. There are a great many choices that need to be made, including whether to have districts at all, whether to represent individuals or groups or interests, how to count votes and declare winners, whether to have secret ballots or voice voting, and whether and how to structure political primaries and ballot access. And this is left largely to statutory law structured for the benefit of particular political interests. The constitutional text does not get us far in this area.

Second, one person, one vote does not prevent gerrymandering and in many ways it facilitates it. Because of one person, one vote, state legislatures are required to redistrict every ten years, and modern technology enables partisan gerrymandering simply to plug the equipopulation constraint into the algorithm.

Third, there is an interdependent relationship between race-based and partisan redistricting. Under the Voting Rights Act, states in certain circumstances are required to create majority-minority districts. Many minorities, especially African Americans, vote overwhelmingly in favor of one party. Stuffing all of the supporters of the minority party into a single district is an effective means of partisan gerrymandering. And so there is a degree to which the Voting Rights Act actually requires a partisan imbalanced map.

Fourth, there is what you might call a baseline problem. Should an ideal map be based on creating competitive districts? Should its overriding goal be to treat the parties the same? Should it be focused on creating a degree of political stability, which might be in tension with competition and with treating parties the same? Should it aim at proportional representation? Note that a perfectly competitive election would make proportional representation quite difficult, since a wave election would cause a small change in support to lead to a large change in the number of seats.

Fifth, voters are not distributed randomly across a polity. Democrats tend to cluster in cities. If you were to use “neutral criteria,” such as maintaining county or other municipal boundaries, the natural tendency might be to pack Democrats and put them at a disadvantage on a statewide map. So you need to have a theory that tells you whether this result is acceptable or not.

Finally, the only way to remove politics from the process is to remove politicians from the process. And so the Court needs to tolerate a certain degree of political control unless it is prepared to say that, contrary to all of American history, independent redistricting is required. Once you say some political control is allowed, the nature of the problem becomes a difference of degree rather than a difference in kind. Courts get very nervous about weighing in on questions of degree.

In sum, policing partisan gerrymandering through the courts is going to be an uphill climb, regardless of what the Supreme Court says in Gill v. Whitford.

For the purposes of this brief discussion, I need to begin by specifying redistricting as a math problem in some way; that is, by formalizing a districting plan as an appropriate kind of mathematical object. I will propose a way to do this that is completely uncontroversial: start with the smallest units of population that are to be the building blocks of a plan–these might be units given by the Census, like blocks, block groups, or tracts, or they might be units given by the state, like precincts or wards.¹ We can represent those population units as nodes or vertices in a graph, and connect two of them if the units are geographically adjacent.

For instance, Figure 1 shows a map of Wisconsin, and with it I have drawn a graph of its 1,409 Census tracts. You certainly can’t see all the ones in Milwaukee by looking at this picture because the graph is too dense there, which illustrates that plotting the graph in this way (with the vertices at the centers of the tracts) also shows you where the population is clustered.

Armed with this, we can say that a (contiguous) districting plan is a partition of the vertices in the graph of a state’s population into some number of subsets called districts, such that each district induces a connected subgraph.² For instance, Wisconsin currently has eight congressional districts and ninety-nine state assembly districts, so if they were made from Census-tract units, then the former districts would have between one hundred and two hundred nodes each while the latter would have only ten to twenty nodes.³

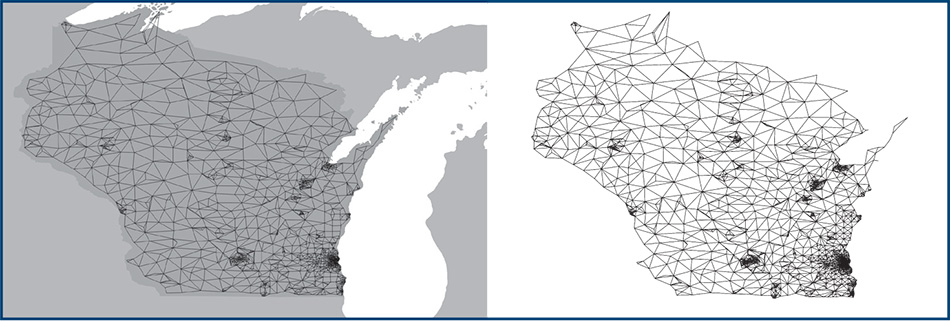
Figure 1. Wisconsin with the Census-tract graph overlaid, and with the graph shown separately.

Our goal when we redistrict is to find a partition that meets a list of criteria. Some of those are universal and apply to the whole country, like having nearly equal populations in the districts and complying with the federal Voting Rights Act, and some are specified by states, such as guidance about shapes of districts or about how much to allow the splitting of counties and cities. Part of what makes redistricting so hard is that many of these rules are vague, and they often represent conflicting priorities.

The rest of this note will be devoted to outlining three intellectually distinct but not mutually exclusive strategies for measuring partisan gerrymandering. The first two are only suited for partisan gerrymandering, but the third is more flexible and can be used for other kinds of measurements of a plan, like racial bias or competitiveness. For each approach, we should track the norm and the baseline: how does the metric correspond to a notion of fairness? What is the basis of comparison against which a plan is assessed?

Partisan symmetry is a principle for districting plans that has been articulated and championed by Gary King, Bernie Grofman, Andrew Gelman, and several other prominent scholars.⁴ At its heart is a certain normative principle (or statement of how fair plans should behave): how one party performs with a certain vote share should be handled symmetrically if the other party received the same vote share. That is, if Democrats received 60 percent of the vote and, with that, won 65 percent of the seats in the election, then if Republicans had earned 60 percent of the vote, they too should have received 65 percent of the seats.

To visualize this, let’s build a seats-votes plot. On the x-axis we will record V, the proportion of votes won by party A. On the y-axis will be S, the proportion of seats in the electoral body won by A. So a single statewide election is represented by one point on this grid; for instance (V, S) = (0.6, 0.65).

The problem is that a single data point does not tell you enough to understand the properties of the districting plan as a plan. A standard way to extend this point to a curve is to use the model called uniform partisan swing: look at the results district by district, and add/subtract the same number of percentage points to party A’s vote share in each district. As you keep adding to A’s vote share, you eventually push the share past 50 percent in some districts, causing those districts to flip their winner from B to A. And as you subtract, you eventually push districts toward B. Thus this method creates a curve that is step-shaped, showing a monotonic increase in the proportion of seats for A as the proportion of votes for A rises.

In Figure 2, we see that the Minnesota election has a seats-votes curve that is very nearly symmetric about the center point (0.5, 0.5). On the other hand, Ohio’s curve is very far from symmetric. Rather, it looks like Ohio Republicans can secure 75 percent of the Congressional representation from just 50 percent of the vote, and that just 42 percent of the vote is enough for them to take a majority of the Congressional seats.

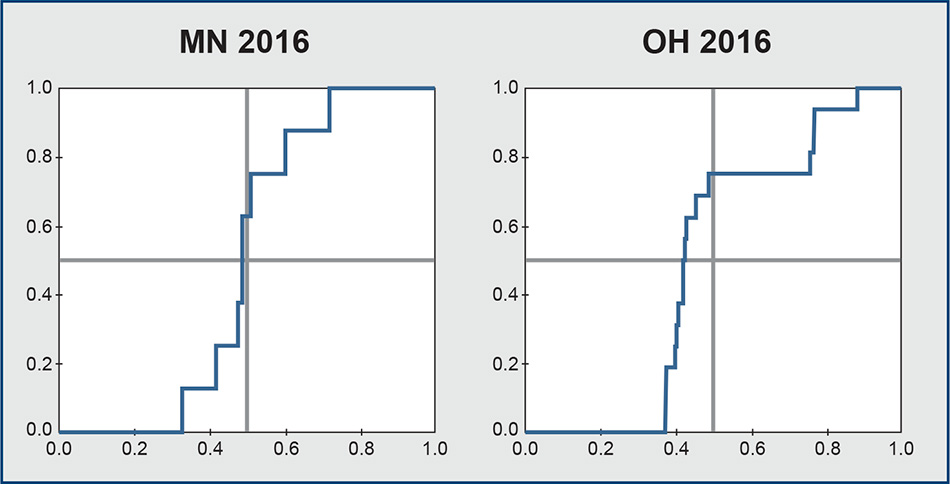
Figure 2. Seats-votes curves generated by uniform partisan swing from the Minnesota and Ohio congressional elections in 2016, both presented from the Republican point of view. The actual election outcomes from which the curves were derived are (0.48, 0.38) for Minnesota and (0.58, 0.75) for Ohio.

A partisan symmetry standard would judge a plan to be more gerrymandered for producing a more asymmetrical seats-votes curve, flagging a plan if the asymmetry is sufficiently severe. There are many ways that a mathematician could imagine using a bit of functional analysis to quantify the failure of symmetry, but there are also a few elementary and easy-to-visualize scores: for instance, look at how far the curve is from the center point (0.5, 0.5), either in vertical displacement or in horizontal displacement, on reasoning that any truly symmetric plan must award each party half the seats if the vote is split exactly evenly. Or compare one party’s outcome with a given vote share to that for the other party if it had the same share.⁵

In the (substantial) literature on partisan symmetry scores, you will sometimes see the vertical displacement called partisan bias⁶ and the horizontal displacement called the mean/median score.

Efficiency gap is a quite different idea about measuring partisan skew, both in its conceptual framing and in which plans it picks out as gerrymanders. However, it does have a whiff of symmetry about it: it begins with the normative principle that a plan is fair if the two parties “waste” an equal number of votes.

In order to parlay a certain given number of party A voters into the maximum possible number of seats for A, an extreme gerrymanderer would want to distribute A voters efficiently through the districts: you would win as many districts as you can by narrow margins, and you would not put any of your voters at all in the districts won by the other side, because they are not contributing toward your representation there. By this logic, there are two ways for a party to waste votes. On one hand, votes are wasted when there is an unnecessarily high winning margin–for this model, say every vote over 50 percent is wasted. On the other hand, all losing votes are wasted votes. Efficiency gap is the quantity given by the following simple expression: just add up the statewide wasted votes for party A by summing over districts, subtract the statewide wasted votes for party B, and divide by the total number of votes in the state. Let’s call this number EG. Note that it is a signed score, and that -0.5 ≤ EG ≤ 0.5 by construction.⁷ By the logic of the definition, a totally fair plan would have EG = 0. This score was first devised by political scientist Eric McGhee and was made into the centerpiece of a multi-pronged legal test by McGhee and law professor Nick Stephanopoulos in their influential 2015 paper. For legislative races, they propose |EG|= 08 as the threshold, past which a plan would be presumptively unconstitutional.

Happily, this test is very easily represented on a seats-votes plot, such as we introduced previously.⁸ The permissibility zone (derived from the EG formula and shown in Figure 3) turns out to be a strip of slope two in the seats-votes space; any election that produces an outcome falling outside this zone is flagged as a gerrymander. That the slope is two means that a certain “seat bonus” is effectively prescribed for the winning side: as the authors of the standard put it, “To produce partisan fairness, in the sense of equal wasted votes for each party, the bonus should be a precisely twofold increase in seat share for a given increase in vote share.” This has the funny property that elections that produce directly proportional outcomes are often flagged as problematic.⁹ For instance, the point (.65, .65), marked in the figure, where a party has earned 65 percent of the vote and converted it to 65 percent of the seats, is seen as a gerrymander in favor of the other side! Quantitatively, that is because this case has EG = .15, far larger than the threshold. Conceptually, it is because the party has received an inadequate seat bonus by the lights of the efficiency gap.

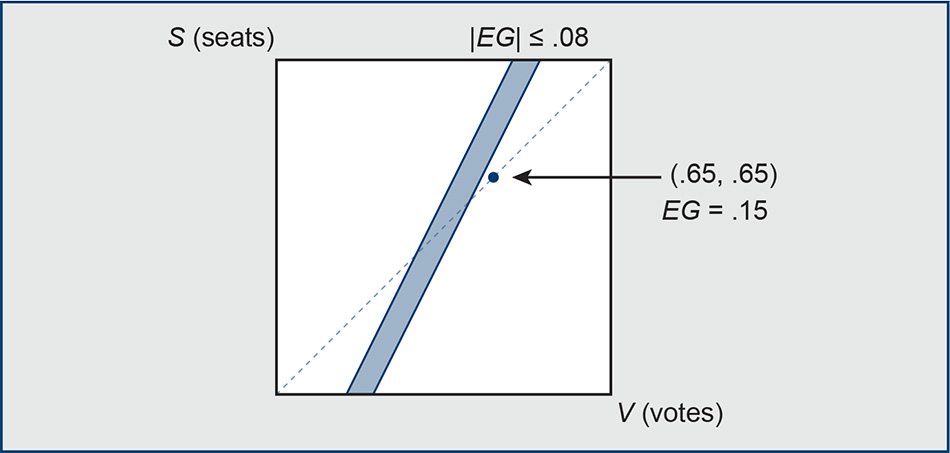
Figure 3. The region containing (S, V) outcomes that pass the EG test is shown in blue. The dashed line is direct proportionality (S = V).

Finally, I want to sketch a new approach to redistricting analysis that has started to crystallize only in the last five or so years. It draws on a very well-established random walk sampling theory whose growth has accelerated continuously since its early development in the 1940s.¹⁰ The scientific details for the application to gerrymandering are still coalescing, but the idea is incredibly promising and has profound conceptual advantages that should cause it to fare well in the courts. This idea is to use algorithmic sampling to understand the space of all possible districting plans for a given state.

Remember our goal: we seek to split up a large, finite graph into some number of districts. What you see in Figure 4 is a very small graph being split up into four districts, represented by the different colors. First, we constrain the search space with requirements for valid plans, such as contiguity of the pieces, compactness of their shapes, keeping population deviation under 1 percent, maintaining the current number of majority-minority districts, and so on. (This will depend on the laws in place in the state we are studying¹¹) A sampling algorithm takes a random walk around the space of all valid partitions: starting with a particular districting plan, flip units from district to district, thousands, millions, billions, or trillions of times.

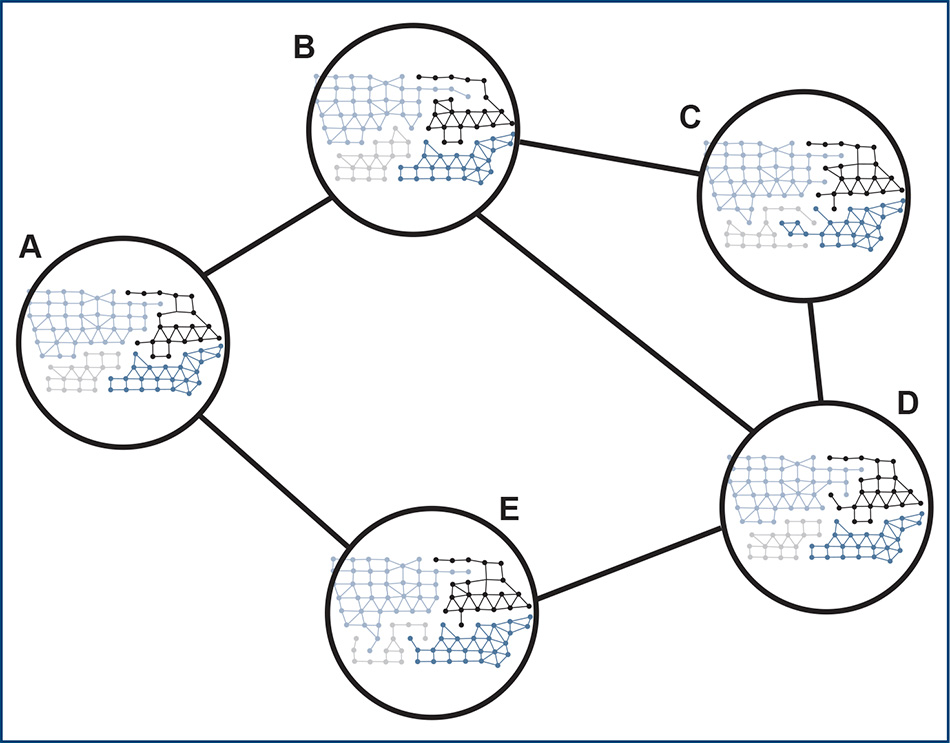
Figure 4. This figure shows a tiny section of a search space of districting plans. Two plans are adjacent here if a simple flip of a node from one district to another takes you from one plan to the other. For instance, toggling one node between light blue and black flips between plan B to plan C.

Searching in this way, such as with a leading method called Markov Chain Monte Carlo, or MCMC, you can sample many thousands of maps from the chains produced by random flips. Each one is a possible way that you could have drawn the district lines. Call this big collection of maps your ensemble of districting plans.

What can you do with a large and diverse ensemble of plans? This finally gives us a good way to address the baseline problem that always looms over attempts to adjudicate gerrymandering. That is, it gives us a tool we can use to decide whether plans are skewed relative to other possible plans with the same raw materials. The norm undergirding the sampling standard is that districting plans should be constructed as though just by the stated principles.

The computer sampling methods could even be used to craft a new legal framework: Extreme outliers are impermissible (see Figure 5). How extreme? That would require some time and experience to determine, just as population deviation standards have taken some time to stabilize numerically in response to the corresponding legal framework of one person, one vote.

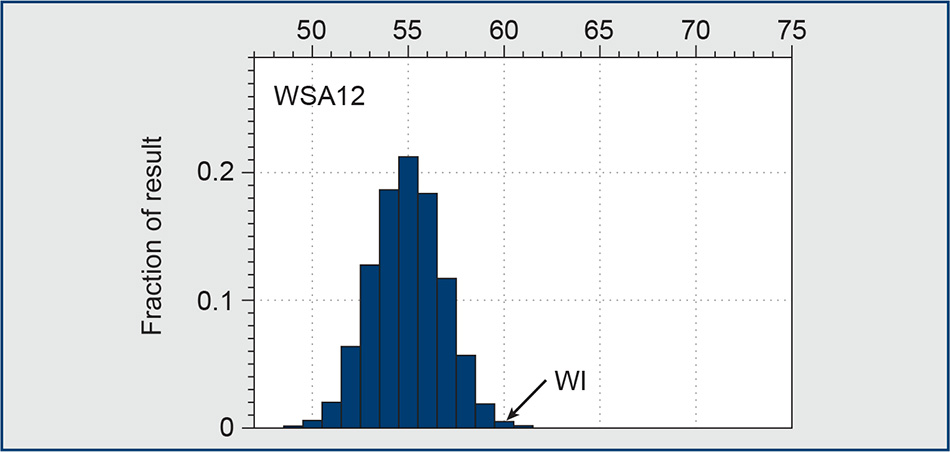
Figure 5. On this plot, the x-axis is the number of seats won by Republicans out of 99 in the Wisconsin State Assembly, and the y-axis shows how often each outcome occurred in the ensemble of 19,184 districting plans generated by the MCMC algorithm from Gregory Herschlag, Jonathan Mattingly, and Robert Ravier, Evaluating Partisan Gerrymandering in Wisconsin, ArXiv. Given the actual vote pattern in the 2012 election, the plans could have produced a number of Republican seats anywhere from 49 to 61, with 55 seats being the most frequent outcome. The legislature’s plan (“Act 43”) in fact produced 60 seats for Republicans, making it more extreme than 99.5 percent of the alternatives.

The great strength of this method is that it is sensitive to the particularities, legal and demographic, of each state that it is used to analyze. If a state has specific rules in its constitution or in state law–examples include North Carolina’s “whole county provision,” Wisconsin’s quirky rules for district contiguity, Arizona’s preference for competitive races, incumbent protection in Kansas, and Colorado’s guidance to minimize the sum of the district perimeters–the sampling can be carried out subject to those constraints or priorities. And just as importantly, it addresses a major critique that can be leveled at both of the previous approaches: why is it reasonable to prefer seats-votes symmetry, or to aim at equal vote wastage, when populations themselves are clustered in highly asymmetrical ways? For instance, imagine a state in which every household has three Republicans and two Democrats. (Of course, this is highly unrealistic, but it is an extreme case of a state with a very uniform distribution of partisan preferences.) Then no matter where you draw the lines, every single district will be 60 percent Republican, which means Republicans win 100 percent of the seats, corresponding to the point (.6, 1) on the seats-votes plot. One can easily verify that there is literally no plan at all that does not have a sky-high partisan bias¹² or that gets the efficiency gap below 0.3. On the other hand, the sampling method will reveal an ensemble in which all plans are made up of 60–40 districts, and thus will show a particular plan with that composition to be completely typical and therefore permissible along partisan lines. It seems intuitively unreasonable for 60 percent of the votes to earn all of the seats, but this method reveals that the political geography of this state demands it.

As mentioned earlier, these three approaches can be used in concert. For instance, one can use any evaluation axis with a sampling ensemble, say efficiency gap (or mean-median score) instead of partisan outcome. So you can mix and match these approaches. Nonetheless, each has a different normative principle at its core and they would produce quite different redistricting outcomes if they were to be adopted at the center of a new legal framework. Let’s review some pros and cons.

For partisan symmetry, it is really easy to make the case for fairness: it sounds eminently reasonable that the two parties should be treated the same by the system. Partisan symmetry uses up-to-date statistics and political science and has a lot of professional consensus behind it. On the other hand, it has been critiqued by the Court as too reliant on speculation and counterfactuals, mainly because of how it arrives at conclusions on how a plan would have performed at different vote levels.¹³ And it does not center on the question of how much advantage the line drawers have squeezed from their power, because it lacks a baseline of how much symmetry a politically neutral agent could reasonably be expected to produce, or even an agent who took symmetry as a goal. Crucially, it is not at all clear that it is easy or even feasible to draw a map that will maintain partisan symmetry across several elections in a Census cycle.

An interesting and attractive feature of efficiency gap is that it seems to derive, rather than prescribe, a permissible range in that seats/votes plot. It offers a single score and a standard threshold, and it is relatively easy to run.¹⁴ The creators of the EG standard did about the best possible job of creating what the courts seemed to be demanding: a single judicially manageable indicator of partisan gerrymandering. It is just important not to elevate EG as a stand-alone metric, since it is trying to address a fundamentally multi-dimensional problem.

Finally, I have described the sampling approach and outlier analysis, and I have argued that the strength of this approach is that it is sensitive to not only the law, as we have seen, but also to the political geography of each state–for instance, Wisconsin Democrats are densely arranged in Milwaukee proper, ringed by heavily Republican suburbs, but in Alaska Democrats are spread throughout the rural parts of the state–which might have hard-to-measure effects on just how possible it is to split up the votes symmetrically or efficiently. Outlier analysis does not measure a districting plan against an all-purpose ideal, but against actual splittings of the state, holding the distribution of votes constant. In the next ten years, I expect to see explosive scientific progress on characterizing the geometry and topology of the space of districting plans, and on understanding the sampling distributions produced by our algorithms.

Note: Many thanks to the American Academy of Arts and Sciences; the other panelists: Gary King and Jamal Greene; and the moderator, Chief Judge Patti Saris. Thanks also to Assaf Bar-Natan, Mira Bernstein, Rebecca Willett, and the research team of Jonathan Mattingly, whose images are reproduced here with permission. I am grateful to Mira Bernstein, Justin Levitt, and Laurie Paul for feedback.

ENDNOTES

1. A districting plan normally will not go below the Census block level, because then the population needs to be estimated. The units in which the election outcomes are recorded are called VTDs, or voting tabulation districts, which typically correspond to precincts or wards. These are natural units to build a plan from if you want to study its partisan properties.

2. It is generally reasonable also to require that no district is wholly surrounded by another district.

3. That is, if the districts were made out of whole tracts. In fact, typically they are made out of finer pieces, like precincts.

4. See Bernard Grofman and Gary King, “The Future of Partisan Symmetry as a Judicial Test for Partisan Gerrymandering after LULAC v. Perry,” Election Law Journal 6 (1) (2007), and its references.

5. If the seats-votes curve is denoted f(V), then this comparison amounts to P(V) = | f(V)–[1–f(1–V)] |. It is natural, for instance, to evaluate this at V = V₀, the actual vote share in a given election, but most authors don’t commit to this.

6. For example, Nick Stephanopoulos and Eric McGhee, “Partisan Gerrymandering and the Efficiency Gap,” University of Chicago Law Review 82 (2) (2015): 831–900.

7. This is true because the total wasted votes in the state, and indeed in each district, add up to half of the votes cast.

8. Note that throughout this section we are leaning on the simplifying assumptions that all districts have equal turnout, there are only two parties, and all races are contested by both sides. These are varyingly realistic assumptions.

9. As mentioned above, EG is proposed as one part of a multi-pronged legal test, so high EG alone wouldn’t doom a plan. But it is obviously still relevant to understand the systematic features of the score and the norms behind its construction.

10. Persi Diaconis’s excellent survey, “The Markov Chain Monte Carlo Revolution,” Bulletin of the American Mathematical Society 46 (2) (April 2009): 179–205, reviews successful applications of MCMC in chemistry, physics, biology, statistics, group theory, and theoretical computer science.

11. The process of interpreting and operationalizing rules to create scores certainly bears scrutiny. A successful implementation will have to demonstrate robustness of outcomes across choices made when scoring.

12. In the simple model, the seats-votes curve is a step function with a big jump at V = 1/2. For more granularity, you could instead imagine a map in which one district has 39 percent Democrats and all others have percentages clustered around 41 percent, also producing a high partisan bias score for no very damning reason. Compare MN-2016 from Figure 2.

13. As Justice Kennedy wrote, “The existence or degree of asymmetry may in large part depend on conjecture about where possible vote-switchers will reside. Even assuming a court could choose reliably among different models of shifting voter preferences, we are wary of adopting a constitutional standard that invalidates a map based on unfair results that would occur in a hypothetical state of affairs.” LULAC v. Perry 126 S. Ct. 2594 (2006).

14. The small print for efficiency gap: you have to worry about which election data to use, and how to impute outcomes in uncontested races, which leaves a little bit of room for the possibility of dueling experts, but by and large it is a very manageable standard.